Lasso and Ridge

릿지ridge 회귀 = 능형회귀 = 티호노프 tikhonov 규제 = L2 노름

\(\star\) 숙지!

릿지 회귀는 L2 규제를 사용하여 모델의 가중치가 커지지 않도록 제한합니다. 이 규제는 일반적으로 극단적인 가중치 값을 갖는 것을 방지하고, 모델의 일반화 성능을 향상시킵니다.

하지만 릿지 회귀는 가중치를 완전히 0으로 만들지는 않습니다. 대신, 가중치를 작게 만들어 모델이 더 일반적인 패턴을 학습하도록 유도합니다. 이는 희소성을 가진 데이터에서 모델의 성능을 향상시키는 데 도움이 됩니다.

반면, 라쏘 회귀는 L1 규제를 사용하여 가중치를 0으로 만들 수 있습니다. 이는 희귀 학습에서 유용합니다. 희소성을 가진 데이터에서는 많은 특성 중 일부만 중요하다는 것을 알 수 있습니다. 따라서, 라쏘 회귀는 이러한 특성을 선택하고 다른 특성을 제거하여 모델을 희소하게 만들 수 있습니다.

Refernece: 책_The Elements of Statistical Learning, 그림과 수식으로 배우는 통통 머신러닝, 2021데이터과학 최규빈교수님 lecture 노트

벌점화모형

기본 가정 : \(\bf{y= X\beta + \epsilon}\) 의 회귀식이 있을때, \(\bf{\hat{\beta} = (X'X)^{-1} X' y}\)로 정의할 수 있음.

의문 : \(\bf{(X'X)^{-1}}\)을 구할 수 없을 때는?
- 1. \(\bf{(X'X)^{-1}}\)가 full-rank 일 때
- 1. \(\bf{(X'X)^{-1}}\)가 full rank 라면 rank = \(p\)
  - \(\to\) \(\bf{(X'X)^{-1}}\)가 존재하지 않는다는 의미는 \(rank(\bf{X'X})<p\)
  - 이유 1) 공선성 때문
  - 이유 2) \(n<p\), 데이터가 부족할 때 이러한 현상이 발생한다.

해결 방법

리지 Ridge

idea : \(\bf{(X'X+\lambda I)^{-1}}\)을 대신 계산한다.

PCA를 이용하여 \(\bf{(X'X)} = \Psi \Lambda \Psi\)로 대신 구함

idea : \(\bf{(X'X)}\) \(\to\) 대칭이고 실수면 \(\to\) 고유 분해 가능
\(\bf{(X'X) = \Psi \lambda \Psi^\top}\)는 \(\bf{(X'X)^{-1} = \Psi \lambda^{-1} \Psi^\top}\)을 의미하니까
- \(\bf{(X'X)(X'X)^{-1}} = I\)

예제)

\(y = \beta_1 x_{i1} + \beta_2 x_{i2} + \epsilon, \epsilon \sim N(0,\sigma^2)_{idd}\)임 모형이 있다고 할 때,

원래 모형은 \(y = 5 x_{i1} + 600 x_{i2}\)이다.

이 때, \(x_{i3}\)이 \(x_{i1}\)과 거의 \(1\)의 상관관계를 가지고 있다면? \(\to\) 다중공선성을 가지고 있다면?

\(\beta_1 + \beta_3 = 5\)만 된다면 원래 모형에 근사하다고 나올 터, 심지어 음수가 나올 때 조차도.

다중공선성의 특징
- 추정하는 \(\beta\)가 어떤 값인지 거의 예측이 안 된다.
  - \(\beta\)들의 분산이 크다. (다양한 값 나오고 그러니..)
- \(\beta\)는 그래도 더하면 원래 값에 근사함.

모두 참이라고 생각되는 모형 \(\to\) 합은 일단 원히던 5임

조건) 다중공선성 없는 \(x_{i2}\)는 \(y\)쪽으로 옮긴 상황. 즉 신경 안 써도 됌

\(\beta_1=2,\beta_2=3\)
\(\beta_1=5,\beta_2=0\)
\(\beta_1=10,\beta_2=-5\)
\(\beta_1=10000,\beta_2=-9995\)

\(\dots\)

-> 음수 있는 해석 불가한 이상한 모형들 다 가능하겠다. 해석 불가능.

Ridge와 Lasso

\(loss = \sum(y-X_1\beta_1 - X_2\beta_2)^2\)

\(loss\tilde{} = (y-XB)^\top (y-XB) + \lambda B^\top B\), \(\bf{\hat{B} = X'X + \lambda I} \to \hat{\beta}\)과 달리 불편추정량이 아님을 알 수 있음

하지만, 분산이 더 작다!
수정된 loss 값 구별 위해 \(\tilde{}\) 기호 추가
\((X'X)\)가 양정치 행렬이라는 조건이 필요하지만, 저절로 만족되어 고려하지 않아도 됌.
\(\lambda\) 잘 찾으면 항상 ridge regression이 linear regression 보다 좋다고 주장할 수 있다.

\(\beta^{QLS} = (X^\top X)^{-1}X^\top Y\)¹

\(\beta^{R} = (X^\top X + \lambda I)^{-1}X^\top Y\)

\((X^\top X)\) 가 역행렬 구할 수 없다고 보고 \(\lambda I\)를 더해줘서 역행렬 구할 수 있게
- 왜냐하면 역행렬 구할 수 없다는 말은 대각선에 0이 존재한다는 것이니까.

벌점화를 주자. = 패널티를 주자 \(loss + \lambda(\beta^2_1 + \beta^2_2)\)

\(\lambda(2^2 + 3^2)\)
\(\lambda(5^2_)\)
\(\lambda(10^2+(-5)^2)\)
\(\lambda((10000)^2 + (-9995)^2)\)

\(\lambda\) = hyperparameter 하이퍼파라메터 = 조율 모수 tuning parameter = Regularization parameter 규제화항

1

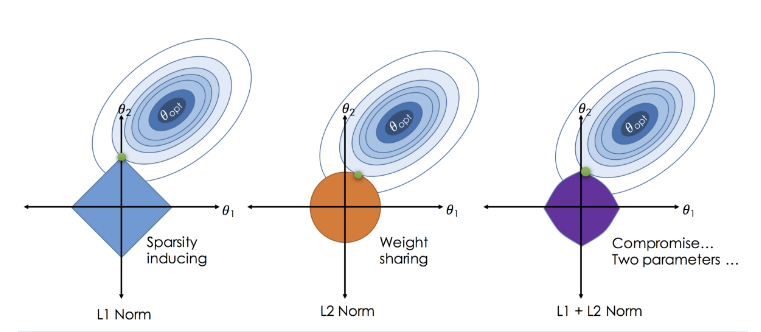
\(loss = SSE + L_2-panalty:Ridge\)

Ridge = \(L_2\) norm = Regularization 정규화 = \(L_2\) 패널티 = 벌점
\((\lambda(\beta_1^2 +\beta^2_2)\)이니까 원 모형이 나오지
- \((\lambda(\beta_1^2 +\beta^2_2) = k\)
- \(\beta_1^2 +\beta^2_2 = \frac{k}{\lambda}\)
\(\lambda\) 가 0이면 loss와 ridge 함수가 만나는 면,
\(\lambda\) 가 \(\infty\)이면 중심(0,0)에 있을터.
너무 큰 \(\beta_i\)들을 구할 때 패널티를 부여하여 되도록 작은 \(\beta_i\)들을 선택하게 제약을 거는 것
가장 최적의 점 \(\beta_1 = \beta_2\)

2

\(loss = SSE + L_1-panalty:Lasso\)

Lasso = \(L_1\) norm
\((\lambda(|\beta_1| +|\beta_2|)\)이니까 마름모 모형이 나오지
- \((\lambda(|\beta_1| +|\beta_2|) = k\)
- \(|\beta_1| +|\beta_2| = \frac{k}{\lambda}\)
\(\lambda\) 가 0이면 loss와 lasso 함수가 만나는 면,
\(\lambda\) 가 \(\infty\)이면 중심(0,0)에 있을터.
가장 최적의 점 \((0,절편), (절편,0)\)

3

\(loss = SSE + L_1-panalty + L_2-panalty : Elastic-net\)

섞어쓰기도 함

\(\lambda \beta^\top\beta\)

패널티항= 벌점항 = L2-패널티, 정규화항이라 부른다.
Ridge(최소제곱학습은 \(L_2\)norm노름에 대한 제약조건 사용)
- \(\lambda ||\beta||^2_2\)로 표현하기도 한다. \(||\dot||_2\)는 벡터의 \(L_2\)-norm노름 이라고 한다.
  - \(x = (x_1,x_2) \to ||x||^2_2 := x^2_1 + x^2_2. ||x||_2 := \sqrt{x^2_1 + x^2_2}\)
  - \(\lambda \beta^\top \beta = \lambda(\beta^2_1 + \beta^2_2)\)
Lasso(희소 학습에서는 \(L_1\)norm노름에 대한 제약조건 사용)
- 희소 학습이라 부르는 이유
  - \(|\beta_1| +|\beta_2|\)해가 0이 되는 구간이 마름모라 4 꼭짓점 나오는데, 이게 희소한 해를 갖는다고 말함

Footnotes

Constrained Least Squares↩︎